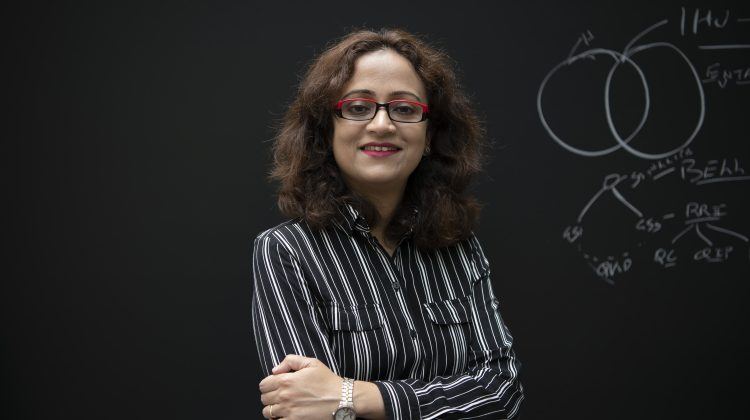Un hypercube de tests de COVID
N’importe quel expert de la santé publique vous le dira : le dépistage est crucial pour vaincre la pandémie de COVID-19. Neil Turok, de l’Institut Périmètre, travaille avec des collègues de l’Institut africain de sciences mathématiques à une nouvelle manière de faire le dépistage sur davantage de personnes en faisant moins de tests. Leurs travaux viennent d’être publiés dans la revue Nature. Les citations de cet article sont traduites d’une entrevue accordée en anglais par M. Turok.

Le cosmologiste Neil Turok est connu pour ses recherches innovatrices visant la compréhension du Big Bang. Il se concentrait sur les rebonds d’univers lorsque la pandémie de la nouvelle maladie à coronavirus a frappé et a changé ses recherches en même temps que le monde.
Titulaire de la chaire Mike-et-Ophelia-Lazaridis-Niels-Bohr de physique théorique de l’Institut Périmètre, Neil Turok est également le fondateur de l’Institut africain de sciences mathématiques (AIMS pour African Institute for Mathematical Sciences), l’un des instituts étroitement associés à l’Institut Périmètre. Bien au courant que ça coûte cher de tester régulièrement tout le monde pour la COVID, et que cela constitue un défi particulier dans les pays en développement, M. Turok s’est joint à une équipe gravitant autour de l’AIMS et qui étudie les tests groupés afin de réduire les coûts. Un article présentant leur nouveau schéma de test vient d’être publié dans la prestigieuse revue internationale Nature.
Aussi appelé « dépistage sur mélange d’échantillons », un test groupé consiste à mélanger les prélèvements effectués sur de nombreuses personnes. L’idée est ancienne — elle a été proposée pour la première fois dans les années 1940, alors que l’armée américaine voulait tester pour la syphilis tous les soldats qui rentraient aux États-Unis —, mais elle n’a jamais été appliquée à grande échelle. Maintenant qu’il est crucial de « tester, tester, tester » pour vaincre la COVID, l’idée des tests groupés est d’actualité.
Le schéma de tests groupés des années 1940 est simple : on divise les gens en groupes, on fait un test pour chaque groupe d’échantillons, puis on teste individuellement toutes les personnes d’un groupe dont le résultat est positif. Le processus est rapide, car il n’y a que 2 rondes de tests, mais il peut exiger un grand nombre de tests, selon la prévalence de l’infection.
L’idée peut être poussée plus loin. En principe, la meilleure manière de minimiser le nombre de tests est de faire une recherche binaire : on répartit un groupe positif en 2 moitiés, et on teste une moitié. Si son résultat est négatif, l’autre moitié est forcément positive. Si le résultat de la première moitié est positif, il faut aussi tester la seconde moitié.
Cette méthode permet de tester le plus grand nombre de personnes avec le moins de tests, mais elle peut comporter une séquence de multiples rondes de tests. Comme chaque ronde de tests peut prendre plusieurs heures, la recherche binaire est souvent trop longue pour être utile contre la COVID.
On a clairement besoin d’un meilleur schéma de tests groupés, qui réalise un équilibre entre le coût et la rapidité. Pour élaborer un tel schéma, Wilfred Ndifon, biologiste mathématicien et scientifique en chef à l’AIMS, et Léon Mutesa, généticien à l’Université du Rwanda et coordonnateur du groupe de travail de ce pays sur la réponse à la COVID-19, ont créé une équipe pluridisciplinaire. M. Ndifon a invité Neil Turok à se joindre à l’équipe pour mettre au point un algorithme qui permettrait de trouver rapidement les personnes infectées, avec le plus petit nombre possible de tests.
L’équipe a conçu ce qu’elle croit être une toute nouvelle méthode de tests groupés, qui repose sur une base géométrique.
Supposons que l’on teste un groupe de 9 personnes placées selon une grille de 3 lignes sur 3 colonnes. On réalise des tests groupés par ligne, puis par colonne. Supposons que l’on obtienne un résultat positif uniquement pour la 1re ligne et la 3e colonne. Cela signifie que la personne qui est sur la 1re ligne et la 3e colonne est infectée. En procédant de cette manière, on obtient les « coordonnées » (ligne et colonne) de toute personne positive parmi un groupe de 9 avec seulement 6 tests en tout.
De la même manière, si l’on dispose 27 personnes selon un cube de 3 × 3 × 3, comme dans un cube de Rubik, on peut obtenir les coordonnées de toute personne positive avec 9 tests. Et il n’y a aucune raison particulière de s’arrêter à 3 dimensions, même si c’est plus difficile à représenter.
« Pour les physiciens, c’est très naturel de travailler dans un grand nombre de dimensions, dit M. Turok. En fait, je crois que nous le faisons un peu trop. Mais dans le cas présent, cela procure un avantage exponentiel. »
Même s’il est plus compliqué de combiner et de coder les échantillons, les avantages mathématiques de ce schéma de test continuent de se multiplier. Un regroupement selon un hypercube à 4 dimensions permet de tester 81 personnes avec 12 tests, et 5 dimensions permettent de tester 243 personnes avec 15 tests.
« Ce nombre est intéressant, parce qu’il avoisine le nombre de passagers d’un avion de ligne, dit M. Turok. Si l’on peut traiter avec un petit nombre de tests les passagers de chaque avion qui arrive, cela devient très avantageux pour la santé publique. »
De fait, ce schéma de tests groupés est maintenant utilisé pour le dépistage des passagers à l’aéroport international du Rwanda. Les prélèvements sont analysés dans le très moderne Centre de génétique humaine de l’Université du Rwanda, dirigé par M. Mutesa.
La méthode est aussi employée pour tester régulièrement les membres d’une des principales équipes de rugby de l’Afrique du Sud et, selon M. Turok, elle va probablement se répandre.
« Nous avons déjà fait la démonstration d’une réduction des coûts d’un facteur de 15 par rapport à des tests individuels, dit M. Turok. Avec d’autres améliorations, des réductions de coût d’un facteur de 100 semblent réalisables. » L’Université d’Édimbourg, où Neil Turok est en congé pour l’année universitaire 2020-2021, planifie un essai à grande échelle en vue d’atteindre cet objectif.
Amener la communauté médicale — sans parler du grand public — à faire confiance à un schéma de tests groupés qui fait intervenir un « hypercube » est un défi en soi. Néanmoins, étant donné les premiers résultats prometteurs et les nets avantages mathématiques de cette méthode, des spécialistes de la santé publique du monde entier commencent à s’y intéresser.
« Nous en sommes au début, mais cela pourrait être révolutionnaire, dit M. Turok. Ce serait alors merveilleux de constater que cela vient de l’Afrique. »