Une expérience jette un coup d’œil furtif sur le monde quantique
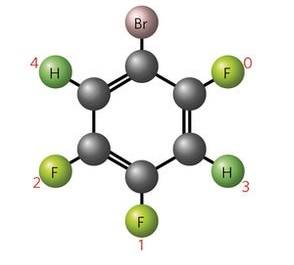
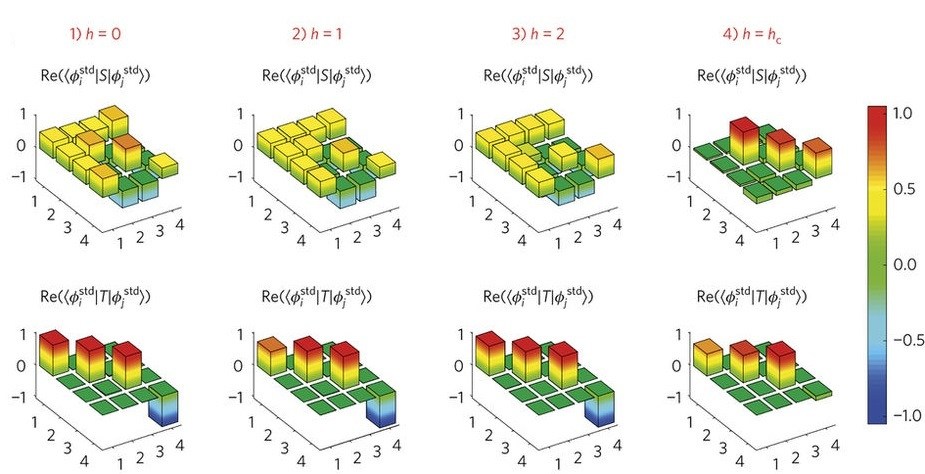
Pour la première fois, des chercheurs viennent d’étudier de manière expérimentale la matière topologique et sa déstructuration. Ces travaux pourraient ouvrir la voie à de nouvelles méthodes de calcul quantique.