Des physiciens quantiques conçoivent un nouvel outil pour étudier les relations classiques de cause à effet

Dans l’imaginaire populaire, les physiciens quantiques sont probablement surtout connus pour leur incapacité à dire si un chat est vivant ou mort. Ils pourraient donc ne pas être considérés comme les plus qualifiés pour démêler les relations de cause à effet et les variables parasites dans des situations comme celle de l’essai à grande échelle d’un médicament.

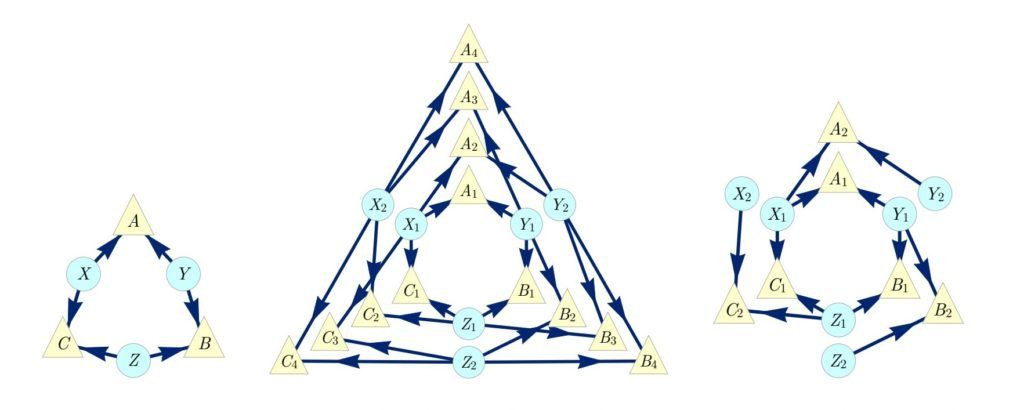
Il se trouve que ce serait une erreur regrettable, puisque 3 chercheurs dans le domaine des fondements quantiques à l’Institut Périmètre viennent de faire une contribution substantielle à l’étude de la causalité.

Dans 2 articles — le premier publié dans le Journal of Causal Inference, et le second actuellement dans arXiv —, ils présentent une nouvelle technique qui aide à démêler une relation complexe de causalité et promet d’être encore plus puissante avec l’accroissement des capacités de calcul.

Robert Spekkens, professeur à l’Institut Périmètre, de même que Tobias Fritz et Elie Wolfe, postdoctorants à l’Institut, ont utilisé des méthodes inspirées par la physique quantique fondamentale afin de créer un nouvel outil qui aide à déterminer, pour des corrélations données, quelles relations de cause à effet constituent des explications viables de ces corrélations

M. Wolfe et Miguel Navascués, de l’Institut d’optique et d’information quantiques de l’Académie autrichienne des sciences, ont ensuite démontré que cette technique permet, en principe, de connaître toutes les contraintes sur les corrélations correspondant à une structure causale donnée (ils ont aussi démontré un important corollaire : plus la précision est grande, plus le coût calculatoire est élevé).

Cela semble être un territoire peu fréquenté par les chercheurs en physique quantique, et c’est effectivement le cas. Les recherches dans le domaine de l’inférence causale (essentiellement la science des causes et des effets) ont traditionnellement été menées par des philosophes, des statisticiens et des informaticiens, ainsi que par des chercheurs dans des domaines tels que l’épidémiologie, l’économie et les sciences de la santé, où les mécanismes de cause à effet ont une grande importance. Aujourd’hui, le domaine de l’inférence causale est peut-être davantage considéré comme une branche de l’apprentissage automatique — de fait, Judea Pearl, pionnier de l’intelligence artificielle (IA) et lauréat d’un prix Turing, a souligné que, pour que l’IA puisse reproduire la manière de penser d’une personne, elle devra pouvoir inclure la compréhension des causes et des effets.

Les physiciens quantiques sont relativement nouveaux parmi les personnes qui s’intéressent à ce problème, mais les travaux réalisés à l’Institut Périmètre montrent qu’ils peuvent apporter une contribution majeure en la matière, avec des répercussions possibles dans tous les domaines où l’on étudie les inférences causales.

Structures de causalité

Il n’est pas toujours aussi facile qu’il n’y paraît de savoir quelle est la cause de quoi. Lorsque l’on trouve une corrélation entre 2 grandeurs observables, il peut être tentant de s’imaginer que l’une détermine l’autre, mais une telle conclusion peut être erronée. Il se peut que la source de la corrélation soit plus profonde et qu’elle réside dans une cause commune invisible qui détermine les 2 grandeurs observables.

L’une des difficultés des relations de causalité vient du nombre quasi illimité de possibilités. Prenons par exemple les données dans le domaine de la santé. Des chercheurs peuvent tester un médicament contre le cancer et obtenir de haut taux de guérison chez les femmes âgées de plus de 60 ans. Mais est-ce parce que le médicament agit, ou parce que la probabilité de rémission spontanée est plus élevée chez les femmes de plus de 60 ans? Sans une analyse attentive — et même parfois avec une telle analyse —, les données ne peuvent dire quel lien est le bon.

Pour se retrouver dans cette jungle de relations de causalité possibles, les chercheurs peuvent se servir de diagrammes de causalité — formalisme visuel qui représente sous forme de graphe l’ensemble (appelé structure de causalité) des relations de causalité possibles.

Les nœuds de ces graphes peuvent décrire des variables de deux types : celles qui sont observées et celles qui sont non observées (ou cachées). Une flèche qui relie 2 nœuds indique une relation directe de cause à effet entre les variables correspondantes.

Les graphes qui comprennent une ou plusieurs variables cachées sont les plus difficiles à analyser, mais on s’attend à ce qu’ils aient le plus d’intérêt pratique — peu importe que le système représenté soit un organisme biologique, l’économie mondiale ou un comportement humain, il y a souvent des facteurs non observés qui sont pertinents dans les relations de cause à effet.

Dans leur article intitulé The Inflation Technique for Causal Inference with Latent Variables (Technique d’inflation pour des inférences causales avec des variables latentes), MM. Wolfe, Spekkens et Fritz proposent une nouvelle technique afin de résoudre la version du problème qui comporte des variables cachées.

Le terme variable cachée est également familier aux physiciens quantiques. Et ce n’est pas un hasard. De fait, l’histoire de la technique d’inflation commence par un résultat phare des fondements de la physique quantique.

Les inégalités de Bell — et au-delà

Dans les années 1960, le physicien John Stewart Bell s’est rendu compte qu’il y a une limite au degré de corrélation possible entre les propriétés mesurées de 2 particules dans un monde classique, c’est-à-dire un monde régi par les lois de la physique classique plutôt que par celles de la mécanique quantique.

Par exemple, si les particules sont séparées par une grande distance, et que la mesure de la première particule est synchronisée avec la mesure de la seconde, dans ce cas même un signal voyageant à la vitesse maximale possible (celle de la lumière) serait trop lent pour informer une particule de la mesure effectuée sur l’autre particule. En supposant que la vitesse de la lumière impose une limite sur la vitesse des influences causales, le choix de ce que l’on mesure sur une particule ne peut avoir une influence causale sur le résultat de la mesure de l’autre particule, de sorte que toute corrélation entre les deux doit être due à une cause commune. Bell a ensuite montré qu’il y a une limite à la force des corrélations pouvant résulter d’une cause commune.

Bell a exprimé cette limite de manière formelle dans les « inégalités de Bell ». Il a aussi démontré que, selon la physique quantique, il est possible de violer ces inégalités. Par conséquent, si un expérimentateur observe des corrélations qui violent les inégalités de Bell, il peut en conclure qu’aucune cause classique ne peut expliquer ces corrélations et qu’il faut obligatoirement recourir à la physique quantique pour expliquer les résultats expérimentaux obtenus. Autrement dit, quelque chose d’intrinsèquement quantique se produit.

Le théorème de Bell constitue depuis 50 ans une clef de voûte des fondements quantiques. En 2015, Robert Spekkens et son étudiant Chris Wood ont publié un résultat très important : ils ont montré que l’on peut utiliser les inégalités de Bell pour déterminer quand les concepts classiques de cause et d’effet ne s’appliquent pas et sont supplantés par les notions quantiques. Cela a contribué au lancement du domaine de l’inférence causale dans la recherche sur les fondements quantiques. C’est ainsi que le trio de chercheurs de l’Institut Périmètre en est venu à travailler sur l’inférence causale.

Les spécialistes des données recherchent également des inégalités qui caractérisent les corrélations compatibles avec une structure de causalité donnée, mais pour des raisons différentes. Lorsqu’un épidémiologiste ou un économiste formule une hypothèse sur une structure de causalité, il s’agit nécessairement d’une conjecture. Pour la prouver, on ne peut certainement pas faire appel à la vitesse finie de la lumière comme dans les expériences semblables à celles de Bell. De plus, les systèmes en cause ne peuvent pas être quantiques. Par conséquent, lorsque leurs données statistiques violent une telle inégalité, la seule conclusion possible est que l’hypothèse initiale concernant la structure de causalité est erronée et doit être révisée.

Étant donné la variété d’hypothèses de causalité pertinentes à des problèmes concrets, les chercheurs aimeraient pouvoir déterminer et identifier les contraintes sur les corrélations concernant n’importe quelle structure de causalité. La recherche d’un algorithme permettant de réaliser cela est un problème ouvert depuis longtemps et d’une grande importance. La technique d’inflation constitue une solution. En faisant appel à la hiérarchie formelle proposée par MM. Wolfe et Navascués, il est possible de découvrir toutes les contraintes liées à une structure de causalité, jusqu’à n’importe quel degré de précision voulu.

La rencontre de deux mondes

MM. Spekkens, Wolfe et Fritz ont tenu à soumettre leur article à une revue du domaine de l’inférence causale plutôt qu’à une revue de physique.

Robert Spekkens explique : « Si ces 2 communautés scientifiques n’ont pas suffisamment de liens entre elles, il y a un risque que les physiciens réinventent la roue sans le savoir. Si l’on soumet ces recherches au Journal of Causal Inference et si celui-ci répond qu’il s’agit de quelque chose de nouveau, alors on peut présumer qu’il s’agit d’une avancée réelle. » [traduction]

En physique quantique fondamentale, on a tout de suite vu l’utilité de la technique d’inflation. Le physicien Nicolas Gisin, de l’Université de Genève, qui travaille aussi bien sur la théorie que sur l’expérimentation en physique quantique, a déclaré : « La technique d’inflation constitue un outil très nouveau et prometteur. Je m’attends à ce qu’elle devienne un outil standard dans mon domaine. » M. Gisin fait toutefois remarquer que cette technique n’en est qu’à ses tout débuts : « Il faut attendre un peu et voir jusqu’à quel point on peut programmer de manière efficace la technique d’inflation et quelle peut être l’étendue de ses applications. » [traduction]

Pour leur part, les experts de l’inférence causale sont enthousiastes. Elie Wolfe a suscité l’engouement lorsqu’il a présenté ces travaux au 7^e atelier sur l’inférence causale organisé dans le cadre de l’importante conférence Intelligence artificielle 2018. À la fin de son exposé, plus d’une douzaine de membres de l’auditoire sont allés le trouver pour lui poser des questions sur la nouvelle technique.

Pour l’informaticien Ilya Shpitser, chercheur de premier plan de l’Université Johns-Hopkins dans le domaine de l’inférence causale, ces travaux constituent une manière nouvelle et originale de réfléchir à un problème central dans son domaine : « Il semble que la technique d’inflation va jeter un éclairage important sur cette question, ou peut-être même la résoudre entièrement. » [traduction]

La technique de l’inflation

Voici en gros comment fonctionne la technique de l’inflation. Le chercheur prend les principales variables causales (dites variables racines) dans le diagramme de causalité original et considère un nouveau diagramme de causalité dans lequel elles sont reproduites plus d’une fois. Cela a pour effet de transformer chaque variable d’origine en plusieurs exemplaires identiques mais répartis de manière indépendante. On peut ensuite réintroduire sur cette base ainsi gonflée les variables dépendantes (celles qui ne sont pas des variables racines) et créer de cette manière un graphe d’inflation dont chaque nœud correspond à un exemplaire d’une variable d’origine dont les causes ont exactement la même structure que dans le graphe original.

La capacité de la technique d’inflation de révéler des inégalités augmente avec le nombre d’exemplaires des variables racines. Cette technique permet en principe de révéler toutes les inégalités impliquées par une structure de causalité donnée.

Avec des ressources informatiques modestes (p. ex. un ordinateur portable), la hiérarchie proposée par MM. Wolfe et Navascués permet d’analyser divers scénarios de causalité en étudiant des graphes d’inflation dans lesquels il y a 2 ou 3 copies de chaque variable racine. La puissance de calcul nécessaire augmente avec le nombre de copies des variables. « On peut parler d’une inflation de niveau 3 lorsque l’on considère 3 exemplaires de chaque variable racine, ou d’une inflation de niveau 4 lorsque l’on considère 4 exemplaires de chaque variable racine, dit M. Wolfe. On obtient ainsi des graphes d’inflation de plus en plus considérables, avec un nombre de plus en plus grand de contraintes de symétrie qui doivent être satisfaites pour en arriver aux conclusions. » [traduction]

Elie Wolfe espère que cette technique fera bientôt partie des outils standard d’étude de causalité, permettant aux chercheurs qui ont des données classiques massives d’étudier en profondeur de petites sections de leurs diagrammes de causalité. Pour les chercheurs en physique quantique, le problème de la certification du caractère quantique des corrélations revêt un grand intérêt, et la technique d’inflation aura probablement des applications en informatique quantique.

« Prenons l’exemple d’un réseau de communication ayant une structure de causalité particulière, dit M. Spekkens. Si vous n’avez pas déterminé les contraintes sur les corrélations qui peuvent être satisfaites de manière classique dans un tel réseau, vous risquez de passer à côté du fait que la physique quantique présente un avantage pour certaines tâches de communication. » [traduction] (Pour comprendre jusqu’à quel point une inégalité quelconque peut être violée dans le cadre de la physique quantique, M. Wolfe et d’autres chercheurs ont conçu une version spéciale proprement quantique de la technique d’inflation, maintenant publiée dans arXiv.)

Un pont est construit

Robert Spekkens fait remarquer que ces idées circulent dans les 2 sens entre les domaines de l’inférence causale et de la physique quantique : « Les notions et le cadre mathématique élaborés par les spécialistes de l’inférence causale fournissent une perspective nouvelle et vraiment prometteuse sur les problèmes conceptuels de la physique quantique. Ils ouvrent tout un ensemble de questions à la réflexion des physiciens quantiques. »

Avec leurs travaux sur la technique d’inflation, les physiciens leur rendent la pareille. De fait, les auteurs de ces travaux s’attendent à ce que les applications les plus importantes de la technique d’inflation concernent des problèmes autres que de physique fondamentale. « Lorsqu’on se rend compte que le théorème de Bell est un exemple de résultat d’inférence causale, dit M. Spekkens, nous voyons que les chercheurs dans le domaine des fondements quantiques ont en fait 50 ans d’expérience en la matière. » [traduction]

L’informaticien Ilya Shpitser voit aussi les avantages d’éliminer les barrières entre disciplines : « En plus de la technique d’inflation, mes collègues et moi-même sommes enthousiasmés de voir un dialogue accru entre physiciens et chercheurs dans le domaine de l’inférence causale. Pour ma part, j’ai déjà beaucoup appris au contact de leur point de vue sur la causalité. » [traduction]

Nicolas Gisin fait écho à ce sentiment : « Le fait qu’une autre communauté scientifique aborde cette question sous des angles différents bénéficiera à la société en général. De nouveaux outils et des étudiants ayant une formation quelque peu différente de celle des experts actuels de l’analyse de données massives pourraient conduire à des percées dans bien des domaines. » [traduction]

REMARQUE : Cet article a été révisé afin de correspondre à l’article imprimé dans le magazine Inside the Perimeter (Dans le périmètre).