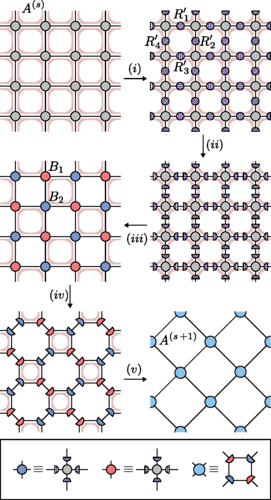
Les réseaux de tenseurs sont de puissants outils. Si seulement les meilleurs fonctionnaient en 3 dimensions!
Voici l’histoire de 3 doctorants et de leur désir de faire tomber la barrière qui empêche les meilleurs outils de réseau de tenseurs de fonctionner en 3 dimensions.