Tensor networks are a powerful tool. If only the best ones worked in three dimensions.

Tensor networks are a hot topic in physics these days. Developed in the 1990s as a tool for condensed matter physics research, the field exploded in the 2000s thanks to ideas from quantum information, and they are now popping up everywhere from field theory to quantum chemistry, holography, machine learning, and more.

What makes them so helpful is that they provide a visual language, and accompanying set of mathematical tools, that simplify fiendishly difficult calculations. But there is a problem: tensor network algorithms currently only work really well for two-dimensional classical models, and by extension, one-dimensional quantum models.

The main issue is computational. Pushing today’s best tensor network algorithms to work in an additional dimension would require more computing power than currently exists. Still, that didn’t stop three Perimeter PhD students from trying to do just that.

For two years, Markus Hauru, Clement Delcamp, and Sebastian Mizera threw themselves at the problem. The resulting paper, “Renormalization of tensor networks using graph-independent local truncations,” was selected as an Editor’s Suggestion when it was published in Physical Review B earlier this year.

The approach they developed is easier to learn and use than the leading existing 2D algorithms, which means it could be adopted more easily by researchers not already acquainted with tensor networks. They did not, however, manage to crack the challenge of taking it to three dimensions.

This not a story of failure, though, says Guifre Vidal, a Perimeter researcher and pioneer of tensor network research. “If anything, this is a story of bravery, leadership, and perseverance by three remarkable young researchers,” he said.

And the students aren’t ready to give up yet. The new approach has become one of the leading contenders for the 2D algorithm that could pave the way for better 3D algorithms. They want to be the ones to take it there.

What is a tensor network?

A tensor network is a mathematical tool used to study the ways that many small objects in a system, such as its particles, combine and behave en masse. This “emergence” of collective behaviour is not just found in physics: everything from ecology to economics grapples with it. (You can see it in droplets of water that create a wave, or the emergence of counter-intuitive behaviours in topological insulators.)

In classical models, a system’s collective behaviour is described by its probability distribution. In quantum systems, it is described by the wave function. These two things are something like keys: knowing a system’s probability distribution or its wave function tells you everything about that system.

The problem is, probability distributions and wave functions can be incredibly complex. For very small systems, the math is manageable. As your system gets larger, however, the computational effort to work out the probability distribution or wave function increases exponentially. A system doesn’t have to be very large before it becomes too difficult for computers to manage.

That’s where tensor networks come in. They can extract the relevant information from a compressed model in order to “zoom out” and see the collective, or “emergent,” behaviour. This offers an efficient way to codify complex structures.

The mid-2000s saw a surge in interest in tensor networks, most from rearchers in quantum information, condensed matter, and statistical physics. This led to the creation of some powerful mathematical tools.

In 2006, Michael Levin of Harvard and Cody Nave of MIT created the tensor renormalization group (TRG) algorithm, which works for classical statistical physics systems.

In 2015, Glen Evenbly and Vidal built on TRG by incorporating ideas that work for quantum systems (called the multiscale entanglement renormalization ansatz, or MERA). The resulting algorithm, called the tensor network renormalization, was capable of addressing much more challenging scenarios, such as when a system undergoes a phase transition.

“TNR is a lot like TRG, and also works for classical statistical physics systems, except that it adds a bit of the special sauce that makes MERA work so well,” Hauru explains.

TNR provides a way to understand emergence by blurring out just enough of the small details so that a broader picture can emerge. It was this approach that caught the eye of the PhD students.

Delcamp and Mizera were working in quantum gravity, investigating the geometry of spacetime at the quantum level. They were using tensor network methods in their work but wanted to explore more advanced techniques.

They reached out to Vidal and his PhD student, Hauru. How, asked Delcamp and Mizera, could they apply the most successful two-dimensional TNR algorithms to their work in three dimensions? The question was met with silence. There was no answer to give.

“We do have 3D algorithms, but they just aren’t as successful as the 2D ones,” Vidal said later. “There is a real need to take the level of success we have at two dimensions, and extend it to tensor networks in higher dimensions.”

So the students set out to do just that.

The quest begins

For six months, Hauru, Delcamp, and Mizera tried to extend the best 2D tensor network algorithms to a higher dimension. Each attempt hit a wall.

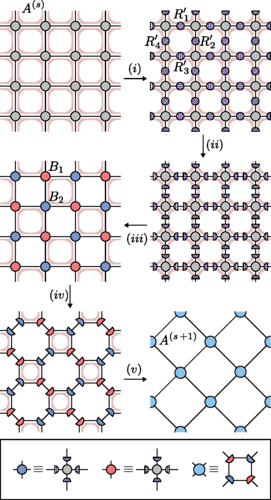
They stopped and took stock of the situation. They realized that TNR was still something of a mystery. Tensor network renormalization acts something like the zoom function on an image display, starting up close with individual pixels and then zooming out to provide the broader picture. During that process, TNR blurs out individual pixels so that a grid of white and black pixels became a blot of grey.

Research had shown that TNR was clearly a very effective algorithm, but how it was doing the “blurring out” was somewhat opaque. The trio had a flash of insight. Instead of trying to generalize an opaque method, they should first try to better understand what was actually going on inside each step. They went back to the drawing board and developed their own approach.

The resulting process uses two separate steps. “You first remove the information which is not relevant, then you do the zooming out,” Delcamp said. “The complicated part is to make sure you don’t accumulate information about the single ‘pixels’ while you zoom out.”

Splitting the process gives the researchers a better idea of what particular roles different tensors play. Some objects remove short-range correlations, others do the zooming out. By having a smaller and more specific task, the tensors become less computationally intense, thereby requiring less computing power.

“Before, it was hard to really identify what each specific tensor you put in your system actually does,” Delcamp said, sketching out a tensor network on a Perimeter chalkboard.

He starts with a map of a system, with lines connecting the individual pieces. Then he overlays it with boxes and chunks spanning the connections between multiple nodes. That, he said, is the old way.

Next to it, he draws their new approach: the boxes and chunks are gone, replaced with small tensors placed directly in the lines connecting individual pieces. (Hauru happily notes that Delcamp’s artistic abilities came in very handy during their collaboration.)

Wiping the dust from his hand, Delcamp said: “With our technique, we believe we have a clearer understanding of what’s going on, which means we can target exactly the action of the tensors we add.”

The result is a simpler, cleaner, and more general algorithm that uses what they call graph-independent local truncations, or “Gilt.” It is just as accurate as its complex predecessors, but does not require the same exhaustive computational load. The team got the algorithm down to 100 lines of code, which they published online for anyone to use.

With growing excitement, they went to extend the new algorithm to three dimensions. It still didn’t work.

Never say never

The “Gilt-TNR” approach developed by the PhD students places smaller tensors in the specific places they are needed. That means the approach does not impact the broader geometry of the system being probed, and that means the approach can be applied to systems with more complex geometry than current TNR algorithms. “It cares much less about the number of dimensions,” the researchers said.

Gilt-TNR could also have more applications than just the “zoom out” renormalization process, said Hauru. “I feel like it could be a useful piece of some other tensor network methods, completely different from this renormalization group stuff,” he said.

Its simplicity, said Vidal, also makes Gilt-TNR a leading contender in the bid to generalize TNR to a third dimension. For him, what makes this incremental advance particularly noteworthy is that the three students did it almost entirely on their own.

“It’s spectacular. This just goes to show how smart PhD students can be,” he said. Vidal paused. “And, I suppose, how unnecessary supervisors are sometimes,” he added with a grin.

Technical improvements are not usually celebrated, but more often than not, it’s these advances that provide a stepping stone to the next major breakthrough. Making it easier to use a highly effective tool is the kind of scientific advance whose dividends might not be fully known for years. Still, the big fish of 3D TNR is still swimming out there.

After two years trying to crack this challenge, the young researchers are taking a well-earned break from this work. Delcamp has obtained his PhD and will soon head to the Max Planck Institute of Quantum Optics. Hauru defends his PhD on Friday, and will then go to the University of Ghent. Mizera is continuing his PhD studies at Perimeter, with his research now veering towards quantum fields and strings.

They haven’t given up hope of one day netting the one that got away and taking their algorithm to 3D. Hauru is keen to dive back in once he’s had a breather. Delcamp and Mizera said they were happy to do the same.

“I think people appreciate the simplicity of it. It’s hopefully a big step towards going to higher dimensions, but in the end we didn’t reach that final goal,” Hauru said.

“Not quite,” said Delcamp.

“Not yet,” Hauru added.