If you can’t make it, fake it: How scientists took a step towards topological quantum computing
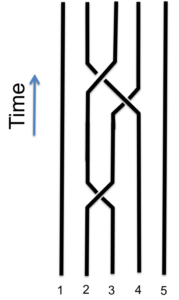
Topological materials hold great potential for quantum computing, but we don’t know how to make them yet. These scientists came up with an alternative: use what we have to simulate what we don’t.