The Bootstrap: Building nature, from the bottom up
Fifty years ago, surf culture reigned supreme, the summer of love was on the horizon, and a revolution started brewing – in physics. Lauren Greenspan tells the story of “the bootstrap”.
Take a self-guided tour from quantum to cosmos!
Fifty years ago, surf culture reigned supreme, the summer of love was on the horizon, and a revolution started brewing – in physics. Lauren Greenspan tells the story of “the bootstrap”.

California, 1960s: Physicist Geoffrey Chew searches for a way to explain the flood of particles discovered by recent collider experiments. Charming and magnetic, he champions the ideas of his collaborators, endowing them with a scope and fervor that sweeps across the nuclear physics community. Instead of the messy, top-down models that piece together the properties of individual particles by hand, his approach aims to discern matter’s constituents as the only ones allowed by consistency principles – pulling themselves up, as it were, by their own bootstraps.
Today, the bootstrap is back as a young group of researchers in Waterloo and worldwide embraces consistency as the underlying tenet of high energy physics. Brutally honest and open-minded, their meetings are a vivacious throw-back to Chew’s bottom-up approach. Though their tools have changed, they use the same central tenets to solve a class of difficult problems. In the process, they aim to discover where “consistency” comes from.
The path from there to here has not been linear. Ideas in science, like objects in space, are inertial. Some remain in constant motion, travelling along paths without incident. But, in nature and notions, unimpeded trajectories are rare. Since its introduction in the 1960s, “the non-perturbative S-matrix bootstrap” has come in and out of fashion, each time prompting a slightly different definition, a reflection of its place within the physics community and history. Now, it appears its time has come.
The mathematical framework that we use to describe elementary particles such as electrons and photons, and their interactions, is known as quantum field theory (QFT). In the 1940s, physicist Richard Feynman drew diagrams to depict how interactions between particles could take place.
When two particles in an accelerator collide, they emit a number (“n”) of particles. The likelihood of any given outcome (for example, that two particles would emerge, shown in equations as n=2), is given by its scattering amplitude. Many things can happen between collision and emission. Particles could come together briefly then split apart. Two particles can combine to create two new particles. Each possibility can be drawn as its own Feynman diagram, and all of the intermediate processes – all of those “in between” possibilities – can be neatly packaged in what is known as the perturbative scattering, or S-matrix.
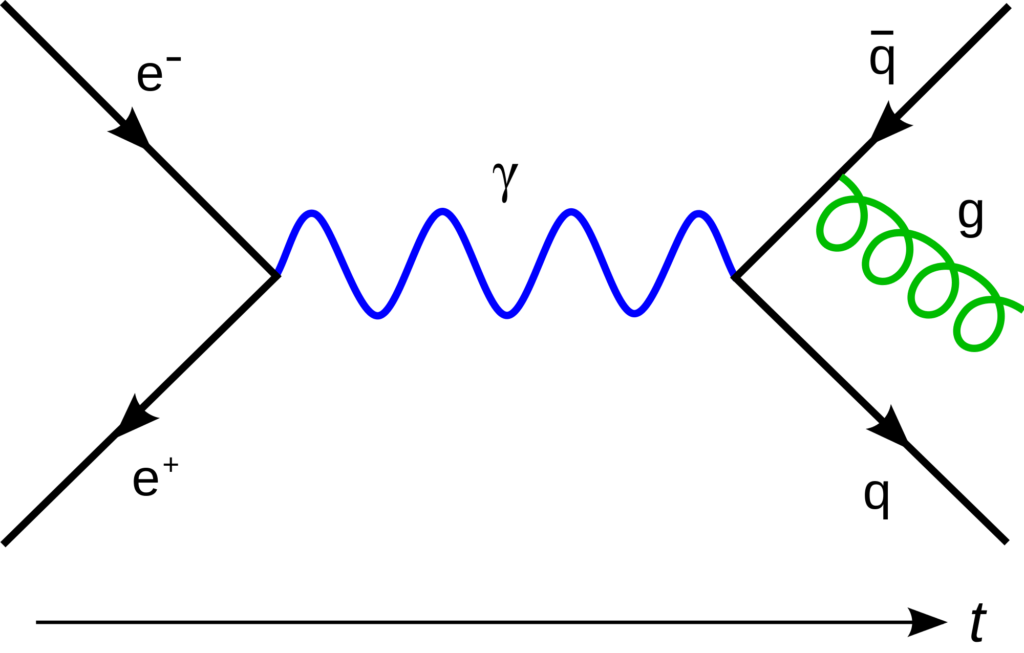
The S-matrix is a compact way to encode the key information of a particle interaction. It can be systematically constructed from Feynman diagrams when the coupling, or interaction strength, between particles in small. In this case, the S-matrix is “perturbative” – particle interactions can be easily ranked and added as smaller and smaller additions to the full S-matrix.
Feynman diagrams act as bookkeepers, visual tools to keep track of the allowed interactions of a particular model. But we must know everything before we can begin drawing them – what particles are involved, and how they couple to each other. Then, one has to draw all possible diagrams and organize them according to their order of contribution. The process is explicitly “top down.”
But when the particles are coupled together strongly — as they are within the nucleus — the intermediate details of the interaction become much more important, and the ledger of Feynman diagram expansions breaks down. A “non-perturbative” formulation of the S-matrix is needed.
Enter the bootstrap.
The bootstrap idea was first proposed in the 1950s as an alternative to Feynman diagrams, a way of demystifying how subatomic particles interacted. In the 1960s, it was developed by Geoffrey Chew, Francis Low, and others. The idea was to use consistency conditions to constrain physical quantities from the outset, leaving only one possible S-matrix to describe strong particle interactions.
Finally, physicists had discovered a non-perturbative alternative to Feynman diagrams. Instead of understanding particle interactions bit by bit in limited circumstances, the bootstrap takes a broader view, providing a way to shed light on the dark corners of nuclear interactions.
The power in the bootstrap point of view lay in the extra information provided by its constraints. Instead of trying to write down the most general expression for a scattering amplitude (from the top down), which was difficult at strong coupling, Chew and colleagues imposed strict limits upon it, such as the restriction that a particle’s future must not affect its past. Another constraint, unitarity, forbids unphysical particles from being exchanged during the intermediate steps of a particle interaction.
The resulting equations could be read as closed circuits of particle masses and couplings that make up a non-perturbative S-matrix. Depending on consistency alone, answers pulled themselves out of the equations by their own bootstraps.
The bootstrap’s biggest success came in 1961, when Chew’s team used it to predict the mass of a single particle, the rho meson, a big win at that time. However, the approach turned out to be successful for only a few special cases, and, therefore, short-lived. Physicists increasingly turned to rigorous new QFT techniques for handling the strong interactions, and the S-matrix program dwindled.
In the 1970s, the bootstrap idea split into two directions. The bootstrap itself was not strong enough to do what it set out to do – given consistency, it could not yet find the right S-matrix or the right correlation functions – but it still held value. The mathematical formulation of S-matrix theory, divorced from the bootstrap techniques, helped to develop modern day string theory. Meanwhile, bootstrap techniques, liberated from their S-matrix applications, went on to become a powerful way to study individual correlation functions of conformal field theories (CFTs).
CFTs are highly symmetric quantum field theories that describe phase transitions, such as when water turns to ice or materials become magnetic. Unlike QFTs, which describe the physics we see day-to-day, CFTs don’t have a scale: they look the same no matter how close or far away you get (or, in a physicist’s words, they are constrained by an additional “conformal symmetry”). The constraint of conformal symmetry makes CFTs easier to study than QFTs. In spite of their simplicity, CFTs are still widely applicable across physics.
In the 1970s, Italian researchers Sergio Ferrara, Raoul Gatto, and Aurelio Grillo tried to unite these additional constraints of CFTs with the old S-matrix bootstrap program. In Russia, Alexander Polyakov did something similar. Combined, their work laid the foundations for the “conformal bootstrap,” as it came to be known.

The conformal bootstrap relied on the formulation of a bottom-up, non-perturbative theory derived solely from first principles. But for theories in more than two dimensions, the equations were so complicated that it seemed the bootstrap was once again doomed to gather cobwebs in the physicist’s wheelhouse.
And yet, the allure of a bottom-up approach based on consistent principles – something so clean and prescriptive compared to the riotous abundance of Feynman diagrams – was too compelling for the idea to completely disappear.
In 2008, Ricardo Rattazzi, Slava Rychkov, Erik Tonni, and Alessandro Vichi found a way to simplify the issue. Instead of seeking unique answers to the conformal bootstrap equations, they devised a way to rule out candidate solutions based on consistency alone. In this way, they were able to delineate the allowed values of physical quantities, such as the mass of a particle exchanged during the intermediate steps in a scattering process. This mapped out not what something is, but what it is not.
Since then, by using new numerical methods and consistency rules, high energy researchers have been slowly plotting out what the physics allows and what it does not. Their laboriously-assembled “exclusion plots,” have systematically whittled away the possibilities into regions of “maybe” and “no.” These plots are perhaps the strongest indication that the bootstrap really might have the power to home in on the physically consistent way to describe the universe.
In 2011, the “Back to the Bootstrap” workshop at Perimeter Institute brought together a small group of young physicists interested in mining this vein. Talks were informal, given on the blackboard instead of with slides, with ample time for discussion and collaboration.
Their methods improved, and the following few years were peppered with successes: papers detailing the bootstrapping of particular correlation functions and surpassing physicists’ expectations by ruling out all but tiny island of consistent solutions. (Remarkably, the remaining, consistent solutions seem to be simple, well-understood theories.) Interest grew and more workshops were arranged. By “Back to the Bootstrap IV”, it was clear that a full-fledged Bootstrap revival was on.
In 2016, a grant from the Simons Foundation brought together a collaboration seeking to exploit the power of non-perturbative bootstrap techniques. A main goal of the collaboration is to use the bootstrap to map out the space of physically consistent CFTs and QFTs.
In a 2016 paper, Miguel Paulos, João Penedones, Jonathan Toledo, Balt van Rees, and Perimeter Institute Faculty member Pedro Vieira argued that the masses and couplings that define a QFT cannot take arbitrary values but are, in fact, related. The coupling of an interaction, they found, is limited by the masses of the interacting particles. This, along with the “no” or “maybe” methods of the conformal bootstrap, was a sufficiently powerful addition to start the old S-matrix bootstrap program up again.
According to Vieira, they set about “carving out the space of possible S-matrices.” Their efforts resulted in several exclusion plots (see Figure 2) that greatly narrowed down the possible massive 2-dimensional QFTs.
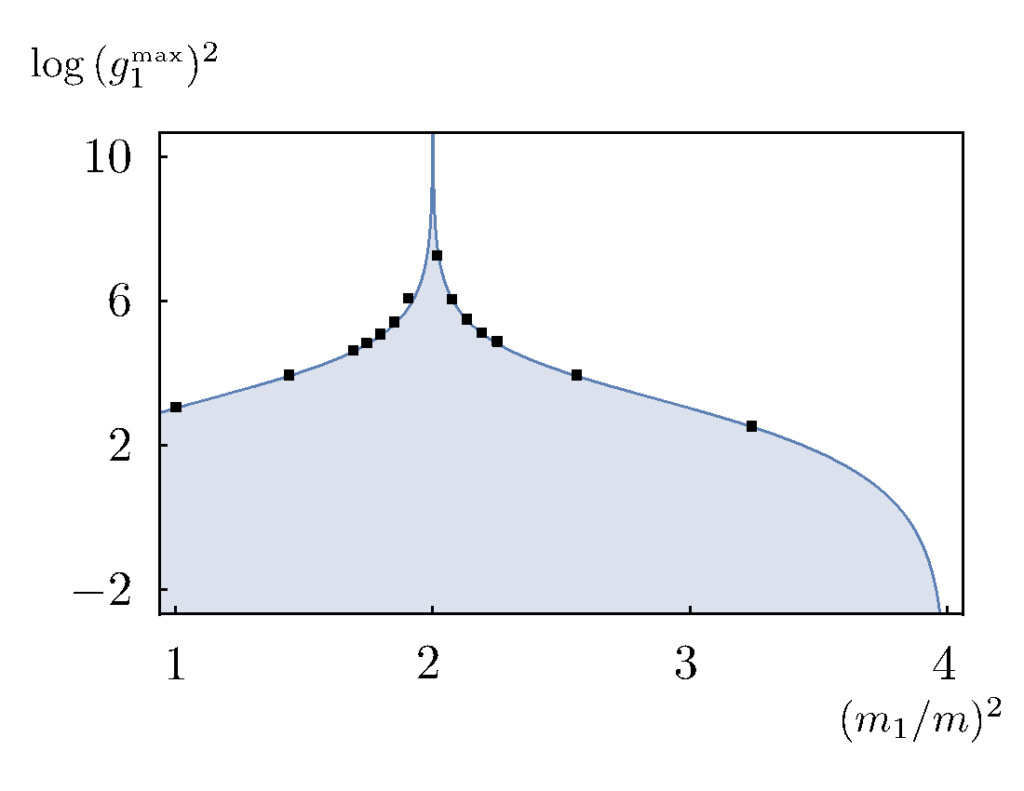
Using the S-matrix bootstrap in this way is clean: it gives a neat result that can be written down without the use of a computer. However, it also requires making an educated guess and hoping that guess is clever enough to get the right answer, or “fix the machine.” To support this new and untested result, Vieira and colleagues studied the same massive 2-dimensional QFTs by relating them to CFTs using a powerful correspondence called holography (see sidebar), thus giving them access to the tried-and-true techniques of the conformal bootstrap.
Holography, also known as the AdS/CFT correspondence, was a remarkable discovery made 20 years ago by physicist Juan Maldacena that translates difficult or intractable problems into ones that are easier to solve. More specifically, it says that a QFT in a special curved space-time called Anti-de Sitter (AdS) space is physically equivalent to a CFT that lives on its boundary. The boundary of AdS is what makes it special: unlike our own flat, infinite universe, AdS is like a more contained, fake universe, making it a useful testing ground for physicists’ thought experiments. Performing difficult calculations in AdS, and then considering what would happen if the AdS boundary were very far away, allows physicists to take advantage of this fake universe while still approximating our own.

Vieira and his colleagues found that holography could indeed transform the problem of a massive QFT into one that the conformal bootstrap can solve. In a pair of papers, the team bootstrapped the same QFTs in two completely different ways. Their results matched incredibly well, highlighting a deep connection between the S-matrix and conformal bootstrap methods.
Using the same bootstrap methods of their first two papers, Paulos, Penedones, Toledo, van Rees, and Vieira more recently explored consistent S-matrices for QFTs in four dimensions, bringing their calculations to a universe more like our own.
The computations in four dimensions are considerably more complex. In two dimensions (one spatial dimension + time), the only information to specify for a particle collision is the energy the particles have when they smash together. In four dimensions (three spatial dimensions + time), one must also factor in the angles between particles when they scatter. As well, making AdS spacetime infinitely large is computationally impossible in four dimensions.
This means that, via holography, the conformally bootstrapped theory is the same as a QFT in AdS; it does not match directly with the S-matrix bootstrap results of the same 4d QFT. Despite the formidable complications, their results provide good qualitative agreement between the two methods.
AdS/CFT “might shed light on these very mysterious assumptions that people were making before,” says Vieira, who recently was awarded the Sackler Prize for his work in QFT. These assumptions – the constraints required of the S-matrix bootstrap – represent both the gift and the curse of bottom-up approaches in physics. By writing down all the laws we think nature should obey, we must hope that nature agrees. The bootstrap does not address why nature behaves this way.
Where do these assumptions come from? What could we be missing? By looking at holography as the bootstrap’s underlying structure, Vieira hopes they’ll be able to probe deeper and ask more questions of possible theories via the S-matrix bootstrap of the future. This represents a novel shift in the way try to understand our universe.
The recent successes of the S-matrix bootstrap have been more than 50 years in the making. Computational advances and keen insight is changing the way we interact with the strongly coupled aspects of our physical world. Bottom-up insights to the QFTs so ubiquitous in today’s physics – from condensed matter to particle physics to string theory – have incredible potential to uncover the secrets of the tiniest particles and the large-scale structure of the universe.
One exciting prospect is to apply the S-matrix bootstrap to quantum chromodynamics (QCD), the particle theory that is thought to best describe our world as we know it. QCD has been waiting for non-perturbative techniques to help us crack its big secrets. At low energies, objects called “glueballs” come into play. Glueballs are strongly interacting balls of particles called gluons, which, according to QCD, are responsible for holding quarks together.
Until now, there have been no tools to study them. The S-matrix bootstrap could one day meet this need by looking at collisions of glueballs and making experimentally verifiable predictions of these important and mysterious objects. That’s just one example. Young, vibrant, and constantly evolving, today’s bootstrap community hopes to exploit all the approach has to offer by fostering collaborations with each other as well as physicists from other fields. The bootstrap comprises a widely applicable set of tools, so computational advancements are one of the community’s key endeavours.
On a deeper level, the bootstrap is also the set of guiding principles behind those tools. Their hope is that by chipping away at fundamental physics in this way, they can ask the universe better and better questions, someday discovering why it behaves the way it does.
“The world didn’t need to behave according to mathematics,” Vieira marvels. “I find it cool that nature is kind enough.”
A thriving new body of research has revived an old tool – the bootstrap – and is using it as a new lens on some of the deepest and toughest problems in field theory.
Researchers cut a vexing problem into manageable shapes, and come up with a solution that could apply to all string theories.
Perimeter researchers have solved a long-standing problem in quantum field theory by mathematically “cutting soap bubbles into pieces.”