Experiment sneaks a peek at the quantum world
For the first time, researchers have experimentally probed topological order and its breakdown. The work could open the way for new approaches to quantum computation.
Take a self-guided tour from quantum to cosmos!
For the first time, researchers have experimentally probed topological order and its breakdown. The work could open the way for new approaches to quantum computation.

Topological matter has been hailed as a potential solution to everything from power transmission to quantum computing. What makes it special – and difficult to study – is quantum.
At a certain point, the long-range entanglement that gives topological matter its special properties breaks down, or decoheres, and it becomes boring old normal matter. This leaves quantum matter researchers facing quite a puzzle: can you identify, let alone observe, the phases[1] of quantum topological matter without destroying the entanglement that bestows its unique properties?
Now, there is an answer: yes, you can. The trick, it turns out, is to have the system do the hard work for you.
In a paper published today in Nature Physics, a team of theorists and experimentalists in China and Canada created a small topological system that, when manipulated slowly enough, revealed its own phases. The researchers also observed the transformation as quantum entanglement broke down.
While the team did its experiment using an NMR machine, they expect that their approach could also work in other physical systems for quantum computers, such as superconductors, and that it could serve as a potential system for quantum memory.
Co-author and former Perimeter postdoctoral fellow Yidun Wan said the results surpassed even the research team’s expectations. “This is something we didn’t quite expect to happen, to observe the breakdown of entanglement so nicely,” said Wan, who is now a professor at Fudan University.
What made it particularly surprising is that the team initially didn’t set out to do any of this at all.
Since topological phases were first put forward as something as a mathematical oddity in the 1970s, they’ve become a hotbed of research activity (and the basis for the 2016 Nobel Prize in Physics).
The China-Canada research team initially set out to find out if two mathematical tools used in topology theory – the S matrix and the T matrix – are actually physical effects that can be experimentally observed.
The S and T matrices are considered one of the most fundamental fingerprints of topological order. They essentially map out what happens when a quantum system is put through a particular transformation. Because topological systems have unique properties, each system’s S and T matrices will be different as well.

Each matrix plots out “anyonic” statistics that represent the behaviour of anyons (an exotic kind of quasiparticle) in a system: the S matrix shows what happens when a quantum system that is mapped onto a torus (which looks like a donut) is rotated; the T matrix defines that same toric system when it is sheared.
In their first experiment, the team used an NMR simulator to show that, indeed, the S and T matrices do provide fundamental signatures of topological order. They sent the paper to Nature Physics for consideration, noting that the result “opens up new future avenues toward identifying more generic topological orders based purely on experimental measurements.”
One of the reviewers sent back a number of pointed questions, chief among them: why didn’t they push the work further?
“The reviewer’s comments were illuminating,” said Wan, who spent the last year of his Canadian postdoctorate working on the research. “We decided to challenge ourselves and try to observe the breakdown of topological order. We redesigned the experiment completely.”
The resulting experiment, and the subject of the new paper, goes well beyond verifying the S and T matrices as an observable fingerprint for topological order.
Now, the matrices have been used to probe topological order itself, mapping out the phases of a system right up to the point where entanglement breaks down, all with minimal theoretical input at the start.
The researchers essentially launched a voyage of discovery. When studying a quantum system, researchers usually calculate the system’s energy interactions and all of its ground states before starting their experiments. This team took a different route.
Theory told them that the system they were simulating – a particular kind of topological code called a Z2 toric code, which is the simplest example of topological order – has four ground states, but they didn’t know what quantum phase those states belonged to. That’s largely because of the quirks of quantum matter.
Quantum systems are described using something called a Hamiltonian. The Hamiltonian is like a map of the energy interactions inside the quantum system. The ground state of a quantum system is the lowest energy it can have while still maintaining its particular Hamiltonian.
But ground states can take different forms, because a system’s Hamiltonian “map” can be configured in different ways: two nuclear up-spins could produce the same Hamiltonian as two down-spins. These alternate versions are called “degenerate ground states,” and they are potentially powerful for quantum memory.
The team decided to use what they had just learned about S and T matrices to see if a simple topological system could essentially identify its own degenerate ground states.
They designed an experiment using the “adiabetic method,” which posits that, if you move slowly enough, you can manipulate a quantum system without disrupting its quantum-ness. (The idea was first proposed in 2008 as a potential avenue for creating quantum memory.) They were essentially sneaking up on a quantum system.
The five-qubit experiment was carried out using a two-dimensional compound called 1-bromo-2,4,5-trifluorobenzene.
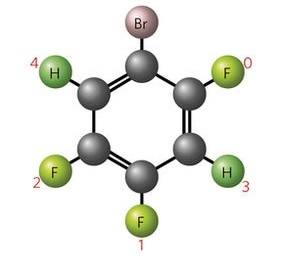
The nuclear spins of two protons and two fluorine atoms were numbered one through four, each serving as a single quantum bit, or “qubit”. A third fluorine atom acted as the observer. (The bromine and carbon-12 nuclei have spins of zero, so cannot be detected by the NMR machine.)
Experimentalist Zhihuang Luo, then a PhD student at the University of Science and Technology of China, used radio-frequency pulses to manipulate the spins of the qubit. Going slowly, he put the four-qubit system through a series of transformations.
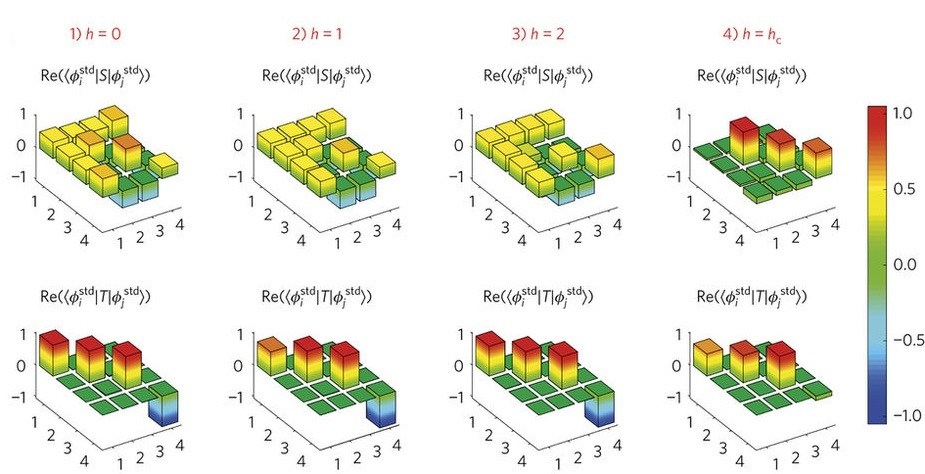
Then, using measurements from the probe qubit, the team developed an algorithm that allowed them to recover the S and T matrices and get a peek at what was happening inside the system as it moved.

“It was difficult. The sample is a liquid crystal that is very sensitive to temperature,” said Luo, who is now a postdoctoral researcher at the Institute for Quantum Computing. “A tiny fluctuation – even 0.1 degree Kelvin – would lead to a large change of the system’s parameters. That decoherence effect is serious.”
Thanks to the observer qubit, the experimentalists were able to monitor the effects of the transformation, and then to recover the S and T matrices from the data, all without destroying the system’s entanglement (or, more technically, without collapsing the wave function).
It seems that sneaking up works. At a critical point, there was a sudden jump and change in the S and T matrices. The system had revealed its information.
The results paint a striking picture: the four degenerate ground states in the Hamiltonian were clearly identified as time evolved, and then the entanglement collapsed. “Our results open up novel avenues toward identifying more generic topological phases purely based on experimental measurements, and open the doors to many applications, like fault tolerant quantum computation,” Luo said.
The experiment shows that, with current technology, researchers can not only identify phases of matter; they can also probe the system in its “phase space,” right up to the point where the long-range entanglement collapses.
This work, Wan said, shows that the idea of using degenerate ground states as quantum memory is sound. It could also be used to identify topological orders in realistic materials, where researchers usually do not have prior knowledge of the topological orders to be discovered nor their ground states.
The researchers said the work also promises to be a better method of characterizing topological order. The standard method – if anything can be called ‘standard’ in this area of physics – is to use entanglement entropy[2]. But this has an inherent flaw: with entanglement entropy, different phases often have the same value. It does not tell you what is happening within a system, because all the phases look alike.
By being able to distinguish between phases, the S and T matrices provide a window to observe quantum behaviour. It could even be used to simulate a quantum computing proposal called anyon braiding, which forms another plank of Wan’s research.
“This is the first time a topological order has been simulated and identified knowing only the approximate Hamiltonian, without any prior knowledge of the ground states,” Wan said.
“The method is here. It’s not only scalable but also applicable to quantum simulators other than NMR simulators. And it becomes more reliable as the system grows. All that is needed now is the technology with which to create it. We need more qubits.”
[1] The phases in normal matter – solid, liquid, gas, plasma – are dictated by temperature. Topological systems also have something called phases, but these are dictated by other factors. At each quantum phase, a topological system obeys specific rules or symmetries. Under certain external pressures, these factors can be altered, and the system can be made to flip from one phase to another. This is called a phase transition.
[2] Entanglement entropy is associated with the information you lose when you isolate a region to study its properties. By “cutting out” part of the system to study, you inevitably lose information about hidden quantum links; this missing information corresponds to entropy.
HEADER ART: “Torus Rainbow” by James Coleman.
Quantum computing will rely on having a working quantum memory, but how can you verify if that memory really is quantum? Three physicists propose how resource theory and game theory could do just that.
Topological materials hold great potential for quantum computing, but we don’t know how to make them yet. These scientists came up with an alternative: use what we have to simulate what we don’t.
New research by Perimeter scientists employs artificial intelligence techniques to explore phases of matter.