Gravity beyond 100: Gravity in a hologram

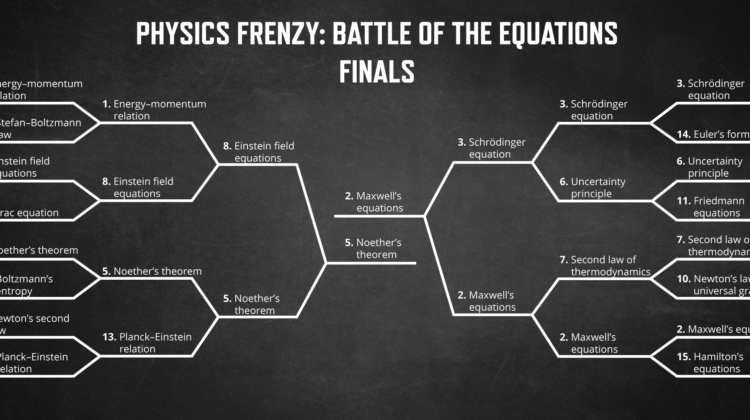
One of the most remarkable ideas to emerge from string theory – which began as an attempt to unify Einstein’s general relativity and quantum mechanics – is known as the AdS/CFT correspondence. This correspondence sets up a mathematical equivalence between quantum systems and objects in a gravitational field. Specifically, it states that gravity in a peculiar kind of spacetime called anti-de Sitter space (or AdS) is equivalent to a special kind of quantum field theory, called conformal field theory (or CFT) in one less dimension. Since this correspondence relates theories in different dimensions, it is often referred to as “holography.” (Recall that a hologram encodes a three-dimensional image on a flat two-dimensional film.)

As absurd as it first sounds, this is an idea that has survived the scrutiny of thousands of theoretical physicists over the past 25 years. One can think of the AdS/CFT correspondence as a bilingual dictionary, which says that there is one set of physical phenomena that can be described by two different languages. One language is gravity, a theory usually used to describe physics on very long scales in terms of geometry and the dynamics of spacetime; the other is quantum field theory, a language that usually describes physics on very small scales in terms of probabilities, wave interference, and particle interactions.

As is often the case with translation, most of the words sound very different in the two languages. A “black hole” in the gravity theory becomes a “thermal plasma” in the quantum field theory. However, sometimes the words have a common root. For instance, the temperature of the plasma corresponds to nothing other than the Hawking temperature of the black hole. (One of Stephen Hawking’s most famous discoveries, made in the 1970s, was that black holes slowly release thermal radiation due to quantum effects near the event horizon.) Much of the research in holography over the past two decades has been detective work to fill out the dictionary.

The holographic equivalence gives us an extraordinary window on both gravity and quantum field theories. The bonus is that in the regime in which the gravity theory is relatively easy to work with, the corresponding quantum field theory is strongly coupled. That is, the standard textbook approaches fail, leaving the theory nearly impossible to work with. Thus we can use holography to calculate for quantum field theories in a regime where we simply had no previous approaches to calculating at all.

The caveat is these holographic calculations apply for special classes of quantum field theories that are not precisely the same as those that describe nature. Despite this, we’ve had some good hints that AdS/CFT provides useful insights and even benchmarks for what we might expect to see in real-world experiments. One of the most celebrated results in this regard states that a holographic plasma behaves like a near-ideal fluid. In technical jargon, we say that its ratio of shear-viscosity-to-entropy-density is extremely low – much lower than in any known fluids. Or it was until 2005, when experimentalists at the Relativistic Heavy Ion Collider discovered that a new phase of nuclear matter known as the quark-gluon plasma was exhibiting almost precisely the same near-ideal fluid behaviour found in holography.

Holographic research is also now reaching out to condensed matter physics, where the theoretical description of many phenomena is hampered by our inability to work with strongly coupled quantum field theories. It is hoped that holographic models may provide us with physical insights into new materials that become superconducting at relatively high temperatures. An important result discovered here at Perimeter through holographic calculations is known as the F-theorem, which tells us something about how all (2+1)-dimensional quantum field theories fit together – the kind of theories that may describe hightemperature superconductors.

In yet another direction, it seems that the physics of black holes may be connected – via holograms – to quantum information. A quantity called “entanglement entropy” has been found to give a measure of the correlations between the microscopic degrees of freedom in a quantum theory. Interestingly, entanglement entropy is a concept that comes from quantum information, where entanglement between the quantum bits (or qubits) is a resource that can be used for ultra-fast computing or ultra-secure communications. Holography encodes the entanglement entropy in the geometry of the spacetime of the gravity theory. This is a remarkable perspective, the implications of which we are still trying to understand.

In the last several years, a broad research program has been launched to bridge quantum information and quantum gravity. It’s becoming one of the most exciting and fast-moving frontiers in physics. All of these results seem to be the tip of an iceberg – holography appears not just to provide a useful set of translational tools, but a whole new perspective. It seems possible that this is the right perspective to reconcile gravity with quantum theory – perhaps the biggest challenge in theoretical physics.

– Robert C. Myers is a founding Faculty member at Perimeter Institute who specializes in quantum fields and strings